Memaparkan angka pada pesawat (definisi)

2024 Pengarang: Leah Sherlock | [email protected]. Diubah suai terakhir: 2023-12-17 05:44

Keupayaan untuk memaparkan bentuk yang berbeza dengan betul pada satah helaian, kanvas dan sebarang permukaan lain adalah kemahiran yang agak ketara. Dan di atas semua itu, ia penting untuk kedua-dua ahli seni: pelukis, pengukir, artis grafik, pereka bentuk (ruang dalaman dan persekitaran seni bina), dan untuk ahli sains: ahli matematik, ahli fizik, pereka bentuk, pencipta.

Tetapi penting juga bagi seseorang yang jauh daripada sfera ini untuk mempelajari cara memahami dan memaparkan dunia di sekelilingnya dengan betul. Ini membantu untuk memahami dengan lebih mendalam semua serba bolehnya. Jika anda tidak mempunyai idea yang mencukupi tentang cara melakukan ini dengan betul, kemungkinan besar anda tidak akan berjaya dalam projek, gambar atau lukisan sebarang ciptaan. Maksudnya, kemahiran ini penting untuk menyelesaikan tugasan harian yang mudah dan untuk tugasan yang mempunyai kepentingan global dan universal.

Sedikit sejarah

Sejak zaman purba, orang telah cuba menggambarkan apa yang mereka lihat di sekeliling mereka: orang lain, beberapa bangunan primitif pada masa itu, dunia tumbuhan dan haiwan yang menakjubkan, gunung yang megah, dan barang-barang ringkas, barangan rumah. Iaitu, dunia dalam semua kepelbagaian dan keagungannya.

Tetapi ketika itu mereka masih tidak tahu bagaimana ia boleh dilakukan dengan tepat dan cekap, sehingga paparan pelbagai objek tiga dimensi pada pesawat benar-benar realistik, hidup. Orang itu tidak mempunyai pengetahuan yang berkaitan dan, lebih-lebih lagi, tiada kemahiran istimewa, kecuali mungkin yang paling asas.

Dikatakan dalam sumber terdahulu bahawa lukisan pertama di dunia hanya terdiri daripada satu baris yang mengikuti bayang-bayang seseorang yang dilemparkan oleh matahari di dinding. Iaitu, alam semula jadi sendiri mencadangkan ke arah mana ia patut bergerak untuk mencari penyelesaian yang betul untuk isu ini.

Dan soalan ini membimbangkan lelaki pada masa itu juga atas sebab ini: dia bukan sahaja mahu mengagumi siluet hidup yang besar, yang asli, boleh dikatakan, tetapi berusaha untuk menangkap objek spatial di atas kapal terbang. Dan dia melakukan ini supaya dengan cara ini dia boleh sama ada menghiasi rumahnya atau tempat yang suci baginya, atau mengambil satu berkas dengan gambar bersamanya dan mengalihkannya ke mana-mana jarak.

Geometri corak

Dan apa sahaja yang anda katakan, tetapi tahun berlalu, berabad-abad berlalu, dan entah bagaimana, apabila tamadun berkembang, orang secara beransur-ansur belajar untuk memaparkan angka yang kompleks dalam ruang dua dimensi, iaitu, di atas kapal terbang. Hanya kini ketepatan saiz dan perkadaran objek yang digambarkan mula kelihatan sangat anggaran.

Tetapi persoalan tentang seberapa betul paparan angka pada pesawat dan berapa banyak ia sepadan dengan isipadu objek asal, pernah menjadi sangat relevan. Dalam beberapa cara, sains baru dipanggilgeometri. Lebih tepat lagi, bahagiannya ialah geometri deskriptif.

Di sini dia hanya mengkaji bentuk dan satah, garis dan titik, serta hubungannya secara relatif antara satu sama lain - kedua-duanya dalam ruang tiga dimensi dan dua dimensi.

Kaedah penukaran

Ciri penting dalam seni visual ialah paparan figura pada satah imej. Lagipun, sebenarnya, ini adalah penangkapan objek spatial tiga dimensi dalam dua dimensi. Iaitu: kompleks mesti ditukar kepada yang ringkas, iaitu objek yang mempunyai panjang, lebar, tinggi mesti dipindahkan ke satah.

Dan geometri deskriptif membuat "peralihan" sedemikian berkat beberapa kaedah. Terdapat kira-kira enam daripadanya secara keseluruhan. Berikut ialah tiga yang utama dan paling popular di seluruh dunia:

• perspektif (apabila objek yang digambarkan dialih keluar dalam ruang);
• unjuran ortogon (unjuran selari, di mana sinarnya berserenjang dengan satah);
• unjuran serong (unjuran selari, di mana sinaran condong berbanding satah).

Objek yang digambarkan kelihatan agak jelas dalam unjuran aksonometrik (yang termasuk ortogon dan serong). Tetapi ia diunjurkan dengan paling jelas dan benar apabila ia ditunjukkan dalam perspektif. Dan kaedah di atas yang sebahagian besarnya menyelesaikan persoalan tentang cara memaparkan angka pada pesawat.

Perspektif

Perspektif mengambil tempat yang paling mulia antara kaedah imej yang lain. Kerana mata manusiaseperti lensa kamera, ia melihat ruang sekeliling dengan cara yang sama. Benda yang jauh dari pemerhati kelihatan lebih kecil dalam saiz, dan kadangkala jauh lebih kecil, berbanding apabila ia dekat.

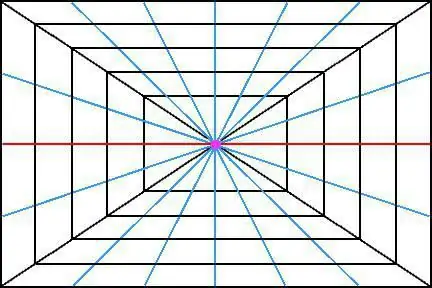
Sebagai contoh, ambil imej kubus di ruang angkasa. Jika, sebenarnya, semua tepinya selari antara satu sama lain, maka apabila anda melihat objek ini dari jauh, ia mungkin kelihatan bahawa tepi menumpu (atau harus menumpu) pada satu titik. Dan, apa yang paling menarik, ia bukan sahaja bertumpu pada satu titik, tetapi mempunyai satu titik persilangan.

Terima kasih kepada pakar zaman Renaissance: Albrecht Dürer, Piero Della Francesca, Andrea Mantegna, Leon Batista Alberti, lukisan moden mengetahui apa itu perspektif linear langsung, cara menentukan ketinggian ufuk dan titik lenyap.

Dan genius yang terkenal di dunia - Leonardo da Vinci - pertama kali berhujah tentang konsep perspektif udara. Ini termasuk perubahan dalam warna, ton objek, perubahan dalam ciri kontrasnya (berkurang apabila objek bergerak menjauh).

Unjuran ortografik

Ortogonal dipanggil unjuran selari, yang diarahkan ke garis lurus, yang berserenjang dengan satah. Dalam proses penggunaannya, dimensi kontur objek kekal tidak berubah. Iaitu, objek dipaparkan tanpa herotan.

Objek tiga dimensi yang diunjurkan, seolah-olah, terurai kepada tiga pandangan: dari sisi, dari hadapan dan dari atas. Dan melihat semua ini pada masa yang sama, anda boleh menambahgambaran tentang rupa objek dalam jumlah. Pada masa yang sama, dimensi rajah kekal tidak berubah dalam imej tiga dimensi dan dalam imej dua dimensi.

Unjuran serong

Unjuran ini dibahagikan kepada beberapa lagi subspesies, iaitu:

• pandangan isometrik;
• unjuran dimetrik;
• unjuran trimetrik.

Isometrik mempunyai pekali herotan dalam kesemua 3 paksi (panjang, lebar, tinggi). Iaitu, sudut antara paksi yang diambil berpasangan adalah sama dengan 120 darjah. Dalam satu dimetrik, herotan di sepanjang 2 paksi adalah sama, dan yang ketiga adalah berbeza. Dan dalam unjuran trimetrik, semua pekali herotan (iaitu, sepanjang 3 paksi) adalah berbeza.

Bentuk putaran

Apabila segitiga bersudut tegak berputar di sepanjang paksi salah satu daripada dua kaki, sisi ketiganya (hipotenus) akan menerangkan angka baharu yang dipanggil kon. Dan jika anda memutarkan segi empat tepat (segi empat sama) di sepanjang salah satu sisinya, anda mendapat silinder. Apabila separuh bulatan berputar, sfera akan keluar.

Ia berikutan bahawa dengan memutar satah sepanjang beberapa paksi, kita mendapat apa yang dipanggil angka putaran.

Angka ini mempunyai paksi putaran. Penampilan mereka di dalam pesawat bergantung pada penempatan mereka berbanding paras mata. Sebagai contoh, bahagian atas dan bawah silinder pada dasarnya adalah bulatan. Dan jika anda melihatnya dalam pesawat, ia kelihatan seperti elips.

Tetapi tugas menjadi lebih sukar jika, apabila dipaparkanangka spatial pada satah, mereka mempunyai paksi condong. Dalam kes ini, adalah penting bahawa kontur badan revolusi adalah sama jarak dari paksi yang terakhir.

Sedikit tentang chiaroscuro

Chiaroscuro memainkan peranan penting dalam memaparkan figura di atas kapal terbang. Kerana kelantangan objek yang digambarkan dicipta bukan sahaja disebabkan oleh garis, tetapi juga disebabkan oleh pengedaran cahaya dan bayang yang betul di sisinya. Kemudian ia kelihatan agak tebal pada satah permukaan dua dimensi.

Oleh itu, paparan angka pada pesawat, menentukan saiznya, ciri tindanan cahaya dan bintik gelap yang betul adalah agak mungkin berkat kaedah di atas. Dan, yang paling penting, ini adalah kaedah yang benar-benar terbukti dalam amalan, yang digunakan oleh pakar terkemuka zaman kita.